tgk

Maximum cliques algorithm in Clojure

A few years ago I was doing molecular comparison algorithms. One way of representing molecules are graphs, and comparing them boils down to finding the biggest common subgraph between two graphs. A well known technique for doing this is by finding the maximum clique of maximum cliques in a graph derived from the two input graphs.

A clique in a graph is a set of nodes such that every node is connected to every other node. A maximum clique is a set of nodes such that no node from the graph can be added without the result no longer being a clique. One algorithm for finding maximum cliques is the Bron-Kerbosch algorithm. As a part of my work, I implemented this algorithm in Clojure, the result is available at github.

In this post I will demonstrate how to use the algorithm, I will describe the original algorithm and the main function in my implementation. This is meant as a demonstration of how a simple algorithm can be implemented in Clojure.

Demonstration

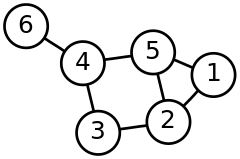
A graph with two cliques

The image above, taken from Wikipedia, demonstrates a graph with five cliques, namely 1-2-5, 2-3, 3-4, 4-5 and 4-6. In Clojure, the graph can be represented as a vector of the nodes 1 to 5 and a map from each node to its neighbours. In our example that is

;; nodes
[1 2 3 4 5 6]

;; neighbours
{1 [2 5]
 2 [1 3 5]
 3 [2 4]
 4 [3 5 6]
 5 [1 2 4]
 6 [4]}

Given this representation and the implementation, the maximum cliques can be found by invoking the function maximum-cliques

user> (maximum-cliques [1 2 3 4 5 6]
                       {1 [2 5]
                        2 [1 3 5]
                        3 [2 4]
                        4 [3 5 6]
                        5 [1 2 4]
                        6 [4]})
(#{1 2 5} #{2 3} #{3 4} #{4 5} #{4 6})

The function works for any seq representation of nodes and any function mapping from node to neighbours, not only maps. The graph above could e.g. be represented in the following manner

(maximum-cliques (range 1 7)     
                 [nil
                  [2 5]
                  [1 3 5]
                  [2 4]
                  [3 5 6]
                  [1 2 4]
                  [4]])

The algorithm

The base algorithm works by growing maximum cliques recursively. The pseudo code from Wikipedia’s entry looks as follows

BronKerbosch1(R,P,X):
       if P and X are both empty:
           report R as a maximal clique
       for each vertex v in P:
           BronKerbosch1(R union {v}, P intersect N(v), X intersect N(v))
           P := P \ {v}
           X := X union {v}

The algorithm simply works by growing the result, using function calls for branching. Implementing the algorithm in Clojure is actually quite straightforward. The following implementation uses a couple of obvious helper functions

(defn bk 
  "Performs the Bron-Kerbosch iterative algorithm."
  [r p x neighbours]
  (if (and (empty? p) (empty? x))
    [(set r)]
    (loop [p p, x x, result []]
      (if (empty? p) 
          result
          (let [v (first p)
                nv (neighbours v)
                result (into result 
                             (bk (cons v r)
                                 (vector-intersection p nv) 
                                 (vector-intersection x nv)
                                 neighbours))
                p (rest p)
                x (cons v x)]
            (recur p x result))))))

In the original pseudo code, results were described as being reported. In the implementation above, this is achieved by maintaining a result vector that accumulates the maximum cliques in the loop. into is used for merging the results as the algorithm progresses. Another difference is that the neighbours function is passed around. A more elegant solution might be to make a higher order function which, given a neighbour function, generates the bk function.

As mentioned previously, the full implementation can be found at github

Conclusion

As demonstrated, implementing the Bron-Kerbosch algorithm in Clojure is fairly straightforward. Algorithm implementations seldomly appear in Clojure posts, so I hope this minor contribrution can retify that slightly.

This implementation is about two years old, and I’m sure I would have done some things differently today if I re-implemented it. However, I still think it is a fairly short and precise implementation of the original algorithm. There are a couple of things that would be interesting to investigate:



comments powered by Disqus