Finding cliques in graphs using core.logic

In this recent post I described a Clojure implementation of the Bron Kerbosch algorithm for finding maximum cliques. In my finishing statement, I mentioned that the Bron Kerbosch algorithm is somewhat similar to the algorithm employed by miniKanren and core.logic when looking for solutions to relational systems. I’ve since implemented a version of the algorithm in core.logic. I guess it’s slightly misleading to say I’ve implemented an algorithm – rather, I have defined, in core.logic, what it means to be a clique and asked core.logic to do the rest of the work!

Definition of cliques in core.logic

In my original post, I investigated the graph presented below:

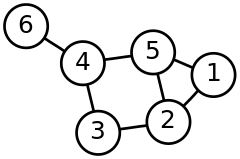
In my Bron Kerbosch implementation, this graph could be represented as the following map:

{1 [2 5]
 2 [1 3 5]
 3 [2 4]
 4 [3 5 6]
 5 [1 2 4]
 6 [4]}

In core.logic, we can define a relation indicating that two numbers are connected, and in that manner describe the graph:

(defrel connected x y)
(facts connected [[1 2] [1 5]])
(facts connected [[2 1] [2 3] [2 5]])
(facts connected [[3 2] [3 4]])
(facts connected [[4 3] [4 5] [4 6]])
(facts connected [[5 1] [5 2] [5 4]])
(facts connected [[6 4]])

To declare that a set of numbers are a clique, every number in the set has to be connected to every other number in the set. A prerequisit to this is, that one number should be connected to every other number in a set. The method connected-to-allo checks that, given an element u and a set of elements l, u is connected to every other element in a recursive manner

(defn connected-to-allo [u l]
  (conde [(emptyo l) succeed]
    [(fresh [a d]
      (conso a d l)
      (connected u a)
      (connected-to-allo u d))]))

Now, given connected-to-allo, declaring the relation that all elements should be connected is done in a similar manner, here in the function all-connected-to-allo

(defn all-connected-to-allo [l]
  (conde [(emptyo l) succeed]
    [(fresh [a d]
      (conso a d l)
      (connected-to-allo a d)
      (all-connected-to-allo d))]))

Now, given second function name and the connection relation on numbers, we can find all the cliques in the graph

user> (run 22 [q] (all-connected-to-allo q))
(() (_.0) (2 1) (3 2) (4 3) (5 4) (2 1 5) (2 3) 
(3 4) (4 5) (1 2) (4 6) (2 5) (1 2 5) (1 5) 
(2 5 1) (5 1) (1 5 2) (5 2) (6 4) (5 1 2) (5 2 1))

The problem is that if we ask for more cliques than there actually is in the system, core.logic is going to continue forever:

user> (run 23 [q] (all-connected-to-allo q)) ;; never terminates
...

That’s a major drawback that I haven’t worked out how to avoid yet. Also, we are given all cliques, not only the maximum. We could probably define a criteria that restricts the size of q so that only big cliques are found and then search for a maximum q instead in the manner of linear program. This doesn’t seem like the right way of doing this, so input as to how to solve optimisation problems with logic programming is more than welcome.

An upside to just having to define the relations is that we can now ask other questions, without having to implement any algorithms. For example, say we wanted to find three cliques containing the number 5

user> (run 3 [q] (all-connected-to-allo q) (membero 5 q))
((5) (5 4) (2 1 5))

Amazing! That’s is certainly one of the most mind-bending things about logic programming: how easy it is to reuse relations and build bigger programs of simple compontents.

Timing

Now for the nasty details: how slow is it? Running the core.logic version on the problem a couple of times yields the following results:

user> (time (run 22 [q] (all-connected-to-allo q)))
"Elapsed time: 1582.675 msecs"
"Elapsed time: 1393.767 msecs"
"Elapsed time: 1422.149 msecs"
"Elapsed time: 1415.158 msecs"
"Elapsed time: 1412.897 msecs"
"Elapsed time: 1403.596 msecs"

Whereas the original algorithm is a fair bit faster, about a factor of a hundred

user> (time (maximum-cliques [1 2 3 4 5 6] neighbour))
"Elapsed time: 1.007 msecs"
"Elapsed time: 0.915 msecs"
"Elapsed time: 0.917 msecs"
"Elapsed time: 1.324 msecs"
"Elapsed time: 0.966 msecs"

Bear in mind that the core.logic version solves a much more general problem, and that it is much easier to combine with other criteria to answer much more interesting problems. For example, you could easily define that all nodes in a clique should be of the same colour, have the same number of outgoing edges, etc…

I would be very interested in getting input on how to solve optimisation problems such as this in core.logic. So far, I’ve only declared what being a clique is, not what being a biggest clique is. Also, I wonder if it is possible to declare that the connected relation is symmetrical.

If you haven’t already, go and check out core.logic. It’s great fun! Here’s an excellent introductory talk, another one, and a great one about miniKanren.

Update

David Nolen, being a gentleman and a scholar, has been so kind as to look into my problem! In this post he adds indexes and, more interestingly, defines an upper bound on the size of an answer. In my problem, any clique’s size is bounded by the total number of nodes, forming a termination criteria. See his blog post for the definition of bounded-listo, and a rewrite of my connected-to-allo and all-connected-to-allo relations.